Krivky

Křivky vyplňující prostor: Z-křivka a Hilbertova křivka

Křivky vyplňující prostor, jako jsou Z-křivka a Hilbertova křivka, jsou důležité nástroje v oblasti počítačové vědy a databázových systémů, zejména při práci s vícerozměrnými daty. Tyto křivky umožňují převod vícerozměrných dat na jednorozměrná, přičemž se snaží zachovat prostorovou lokalitu. To znamená, že body, které jsou blízko sebe ve vícerozměrném prostoru, zůstanou blízko sebe i v jednorozměrném pořadí.

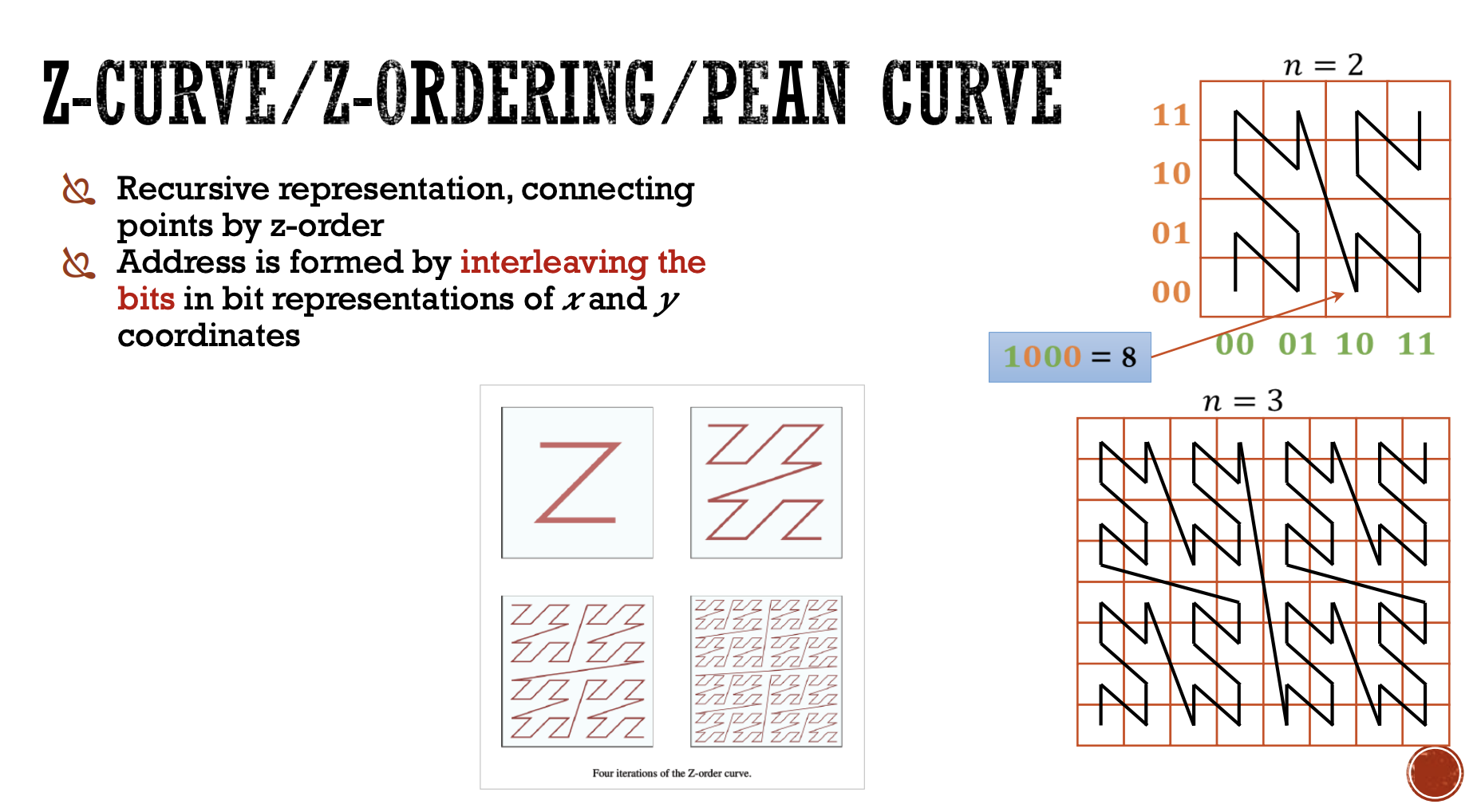
1. Z-křivka (Z-order)

Z-křivka, také známá jako Lebesgueova křivka, se vytváří tak, že prostor (např. dvourozměrná mřížka) se opakovaně dělí na čtyři kvadranty, přičemž se prochází jednotlivé body ve tvaru "Z". Tento proces se rekurzivně opakuje v každém kvadrantu, což vytváří strukturu podobnou zubatému tvaru, která prochází všechny body mřížky.

Výhody Z-křivky:

• Jednoduchost implementace: Z-křivka se dá snadno implementovat pomocí interleavingu bitů x a y souřadnic.
• Efektivní indexování: Umožňuje efektivní mapování dvourozměrných dat na jednorozměrné indexy, což je užitečné pro ukládání a vyhledávání dat ve standardních datových strukturách, jako jsou B+ stromy.
• Lokalita: I když Z-křivka nezachovává lokalitu stejně dobře jako Hilbertova křivka, stále udržuje relativně dobrou lokalitu bodů, což je užitečné pro některé typy dotazů.
  

2. Hilbertova křivka

Hilbertova křivka je komplikovanější než Z-křivka, ale lépe zachovává prostorovou lokalitu. Hilbertova křivka je vytvořena rekurzivním rozdělením prostoru na čtyři části, přičemž se při každé iteraci křivka přizpůsobuje tak, aby co nejvíce sousedních bodů v prostoru zůstalo sousedními i v jednorozměrném pořadí.

Výhody Hilbertovy křivky:

• Lepší zachování prostorové locality: Hilbertova křivka zajišťuje, že body, které jsou blízko sebe v dvourozměrném prostoru, zůstanou blízko sebe i v jednorozměrném prostoru, což je klíčové pro efektivní zpracování dotazů ve vícerozměrných datech.
• Vhodné pro databázové operace: Hilbertova křivka je ideální pro databázové systémy, které využívají vícerozměrné indexy, protože zlepšuje výkon dotazů, které závisí na prostorové lokalitě.
  

Vizuální znázornění

1. Z-křivka:

   • Představte si mřížku 4x4, kde se body procházejí ve tvaru "Z". Začínáme v levém horním rohu, pokračujeme doprava, pak dolů do dalšího kvadrantu, a poté zase zpět doleva, čímž se pokryje celá mřížka.

2. Hilbertova křivka:

   • Podobně jako u Z-křivky začneme rozdělením prostoru na kvadranty, ale místo jednoduchého Z-tvaru, Hilbertova křivka prochází body složitějším způsobem, aby maximalizovala sousedství bodů.

Shrnutí

Z-křivka a Hilbertova křivka jsou obě důležité pro převod vícerozměrných dat na jednorozměrná. Zatímco Z-křivka je jednodušší na implementaci a stále poskytuje dobrou lokalitu, Hilbertova křivka nabízí lepší zachování prostorové locality, což je klíčové pro výkon vícerozměrných databázových dotazů. V databázových systémech jsou tyto křivky využívány pro efektivní indexování a zpracování prostorových dat.