Pravdepodobnost a statistika
Poznámky jsou od Tomáše Slámy, kde jsou upravený do tohohle formátu pro tisk
Úvod
Definice (prostor jevů) je
a - je uzavřený na doplňky:
a - Jinými slovy, pokud se jev A stal patři do
, to znamená, že i jev A se nestal patři do
- Jinými slovy, pokud se jev A stal patři do
- je uzavřený na sjednocení:
Elementární jevy jsou nejjednodušší možné výsledky náhodného pokusu. Jde o výsledek, který nelze dále rozdělit na menší části.
PříkladPředstavme si například házení mincí. V tomto případě existují dva elementární jevy: padne hlava
nebo padne orel . Tyto jevy jsou elementární, protože každý z nich představuje základní výsledek, který nemůžeme rozložit na menší části. Celý prostor všech možných výsledků, tedy množina , se nazývá vzorový (nebo také pravděpodobnostní) prostor.
Definice (Náhodný jev):
Definice (pravděpodobnost) je funkce
a pro libovolnou posloupnost po dvou disjunktních jevů
Definice (pravděpodobnostní prostor) je trojice
je libovolná množina (prostor elementárních jevů), je prostor jevů, a je pravděpodobnost přiřazující každému jevu pravděpodobnost.
Příklad (pravděpodobností prostory):
- konečný s uniformní pravděpodobností:
je libovolná konečná množina, - diskrétní:
je libovolná spočetná množina - spojitý:
, vhodná, definován přes integrál (viz dále)
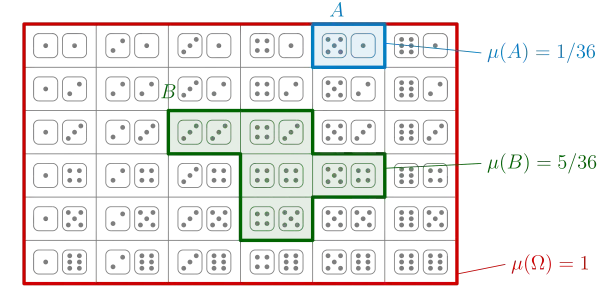
Znázornění konečného prostoru s uniformní pravděpodobností. dvojice hodů kostkou jsou elementární jevy (
Lemma (základní vlastnosti):
=
Definice (podmíněná pravděpodobnost): pokud
Věta (o úplně pravděpodobnosti): *Pokud
Definice (rozklad): spočetný systém množin
pro a
Věta (rozbor všech možností): *Pokud
Věta (Bayesova): *pokud
Věta řeší problém, kdy máme jev
což intuitivně dává smysl – při pravděpodobnosti
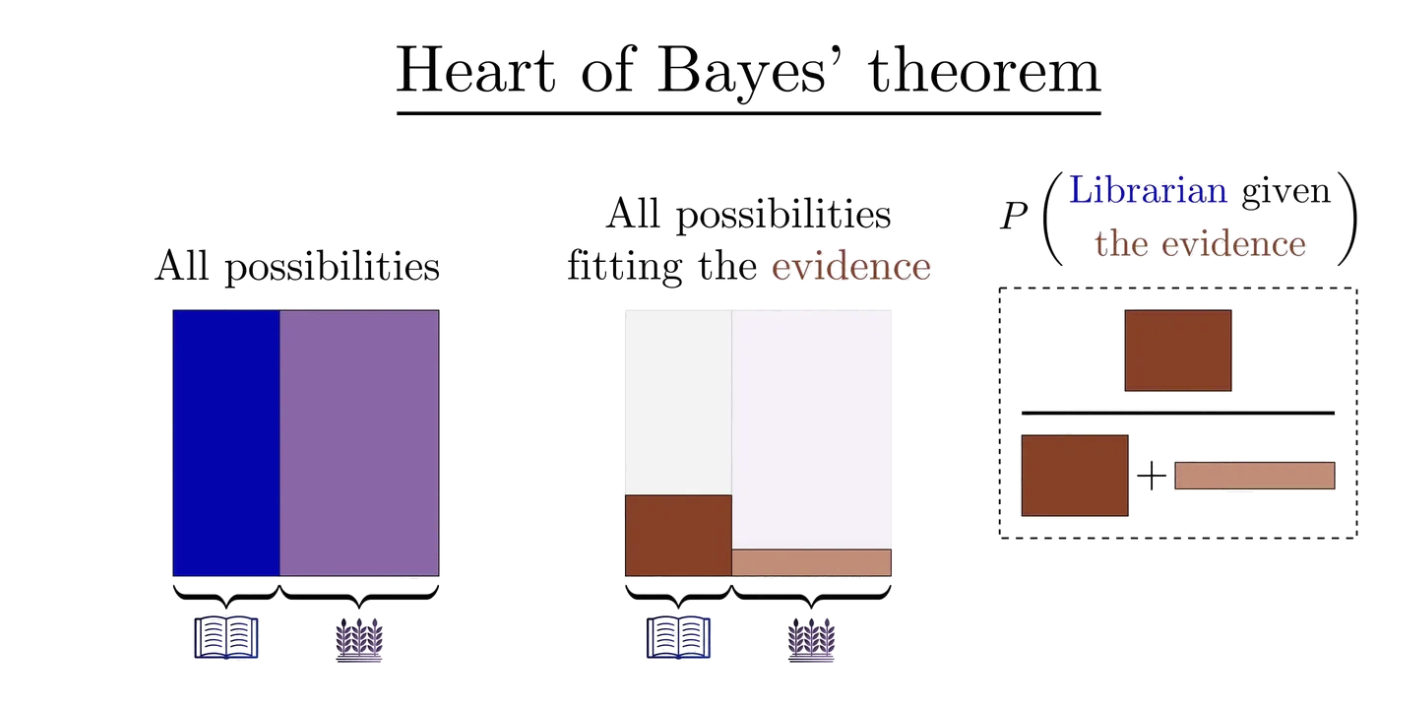
3b1b udělal o Bayesově větě pěkné video, ze kterého jsem vykradl obrázek výše.
Definice (nezávislost jevů): dva jevy jsou nezávislé, pokud
Diskrétní náhodné veličiny
Definice (diskrétní náhodná veličina): Pro pravděpodobnostní prostor
Příklad (použití náhodných veličin):
- hodíme na terč a měříme vzdálenost od středu
- házíme kostkou, dokud nepadne šestka a pak nás zajímá počet hodů
Definice (pravděpodobnostní funkce) (pmf) diskrétní náhodné veličiny
Rozdělení
Bernoulli
počet orlů při jednom hodu nespravedlivou mincí (značíme ) a , jinak
Binomiální
počet orlů při hodech nespravedlivou mincí (značíme ) - méně očivivně
- chceme, aby se
hodů trefilo a netrefilo
- chceme, aby se
Poissonovo
- limita
, popisuje např. počet mailů za hodinu
Geometrické
kolikátým hodem mincí padl první orel (značíme ) - chceme, aby se prvních
hodů trefilo a poslední netrefil
- chceme, aby se prvních
Střední hodnota
Definice (střední hodnota diskrétní n.v.)
pokud součet dává smysl.
Věta (LOTUS): *pokud
Lemma (vlastnosti střední hodnoty): nechť
- pokud
a , tak - pokud
, tak (linearita střední hodnoty)
Definice (rozptyl/variance) n.v. nazveme
- má intuitivní význam – jedná se o očekávanou vzdálenost (
) od střední hodnoty
Definice (směrodatná odchylka) je
Věta:
Přehled parametrů známých rozdělení:
| Rozdělení | ||
|---|---|---|
Sdružené rozdělení
Definice: pro diskrétní n.v.
(👀): z
Definice (nezávislé náhodné veličiny): veličiny
neboli
Věta (součin n.n.v.): *pro nezávislé diskrétní veličiny
Definice (podmíněné rozdělení): pro
Příklad: Pro
| 10 | 11 | 12 | ||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 |
| 10 | 11 | 12 | ||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 |
Spojité náhodné veličiny
Definice (náhodná veličina) na
(👀): diskrétní n.v. je náhodná veličina (pro tu platí rovnost, kterou posčítáme).
Definice (distribuční funkce) (DNF) n.v. je funkce
(👀):
je neklesající je zprava spojitá
Definice (spojitá náhodná veličina): n.n.v. je spojitá, pokud existuje nezáporná reálná funkce
Rozdělení
Příklad (uniformní rozdělení): n.v.

Příklad (exponenciální rozdělení): n.v.
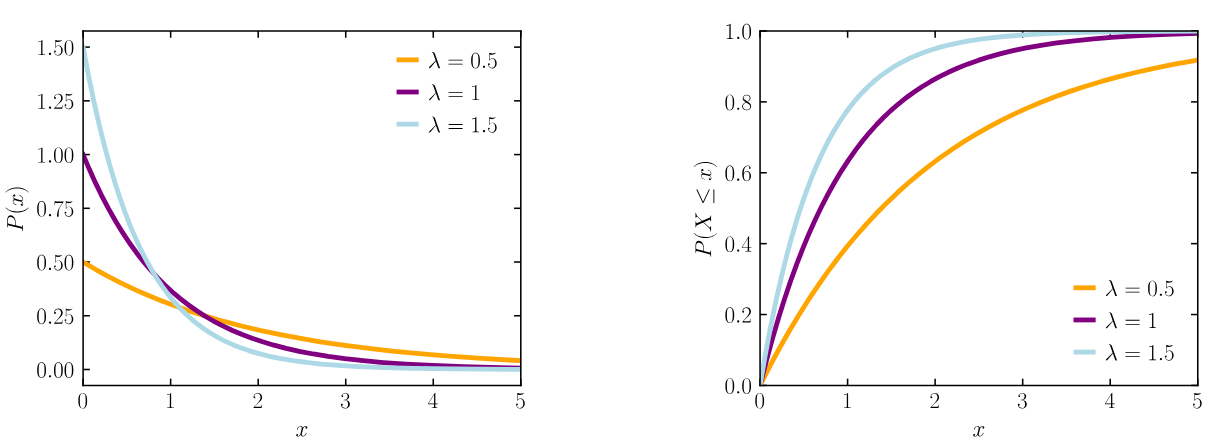
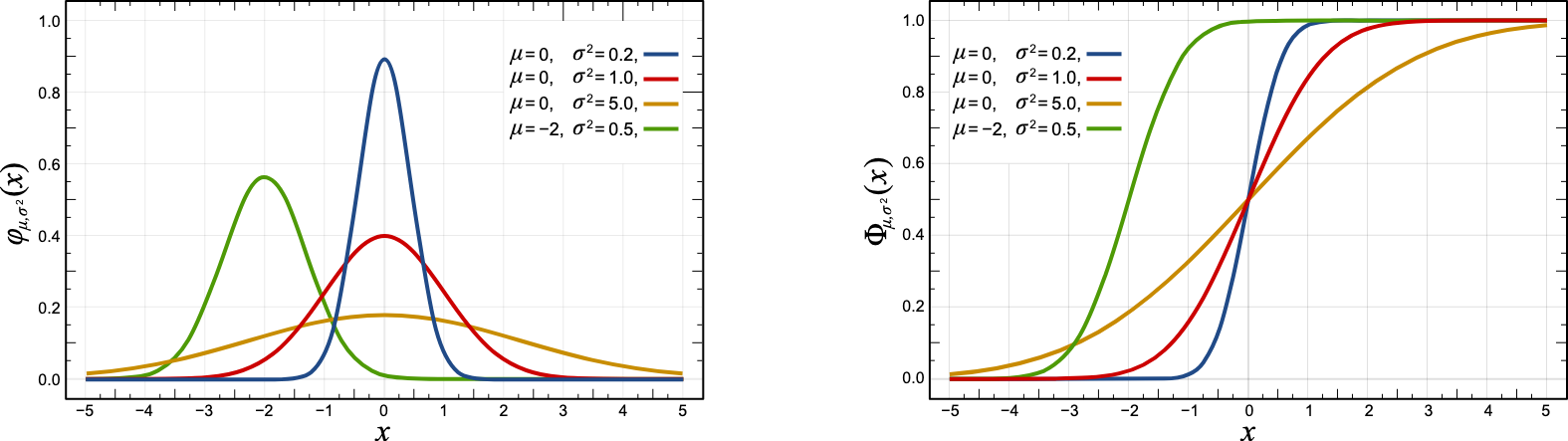
Příklad (normální rozdělení): n.v.
Definice (kvantilová funkce): pro distribuční funkci
(👀): pokud je
Definice (střední hodnota s.n.v.) je definována jako
pokud integrál dává smysl.
Poznámka: LOTUS, linearita, rozptyl fungují také (přesně tak, jak bychom čekali)
Definice (kovariance): pro n.v.
Lemma:
nezávislé
Nerovnosti
Věta (Markovova nerovnost): *nechť náhodná veličina splňuje
(👀): říká, že pravděpodobnost, že
- pro
může být střední hodnota nejhůř vždy - pro
dostáváme – kdyby byla střední hodnota častěji než , tak posčítáním přes všechny hodnoty dostáváme spor, střední hodnota by musela být vyšší
Limitní věty
Věta (zákon velkých čísel): *nechť
skoro jistě (tj. s pravděpodobností
Věta říká, že je smyslupné průměrovat n.n.v. (s větším
Věta (centrální limitní věta): *nechť
Tedy (vhodně přeškálovaný) součet n.n.v.
Tahák
Ke zkoušce byla povolena A4 s libovolnými poznamkami, tady jsou moje (dostupné i v PDF).
![[tahak.pdf]]